2025. 4. 3. 19:57ㆍ카테고리 없음
문제
십자 모양인 골렘을 탄 정령이 숲을 아래, 왼쪽+아래, 오른쪽+아래의 세가지 방법으로 숲을 더이상 탐색할 수 없을 때까지 탐색한다. 탐색이 끝난 골렘의 가장 낮은 행을 더해나아가는 문제이다.

풀이 방법
- 시간 : 3시간 30분
- 접근 방식 : BFS + 시뮬레이션
기능은 크게 2가지로 나눴다.
- 골렘의 이동
- 아래로
- 왼쪽 + 아래
- 오른쪽 + 아래
- 위 세 조건 다 이동하지 못한다면 끝
- 골렘의 중심 좌표가 숲 바깥이라면 초기화 진행
- BFS로 제일 낮은 행 찾기
구체적인 설명
이 문제에서는 무조건 골렘의 중앙값을 가지고 모든 계산을 진행하면 된다.
나는 먼저 문제를 보자마자 골렘의 모양부터 확인했다.

골렘의 모양은 위 사진과 같이 네 가지만 생설될 수 있었고 상, 하, 좌, 우, 중앙 좌표를 이용해 골렘을 그려줘야겠다고 생각했다. 골렘을 그리기 위해 상, 하, 좌, 우, 중앙 좌표를 나타내는 2차원 배열과 골렘의 모양을 나타내는 2차원 배열을 만들어주었다.
static int[][] place = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}, {0, 0}}; //상, 하, 좌, 우, 중앙
static int[][] golem = {{2, 1, 1, 1, 3},
{1, 1, 1, 2, 3},
{1, 2, 1, 1, 3},
{1, 1, 2, 1, 3}};
for(int i = 0; i < 5; i++){
int nx = x + place[i][0];
int ny = y + place[i][1];
forest[nx][ny] = golem[ndir][i];
}
아래 for문을 이용해 앞으로 상, 하, 좌, 우, 중앙 위치를 계산해 해당 dir모양의 골렘을 숲에 넣어주도록 구현했다.
이제 골렘의 이동을 확인해야 했다.
골렘의 이동
1. 아래로 이동

아래로 이동같은 경우에는 초록색 칸이 빈칸으로 존재해야했다. 골렘의 중앙값을 이용해 확인해야하기 때문에 화살표가 그려진 칸을 확인하면 된다.
2. 왼쪽 + 아래 / 오른쪽 + 아래 이동
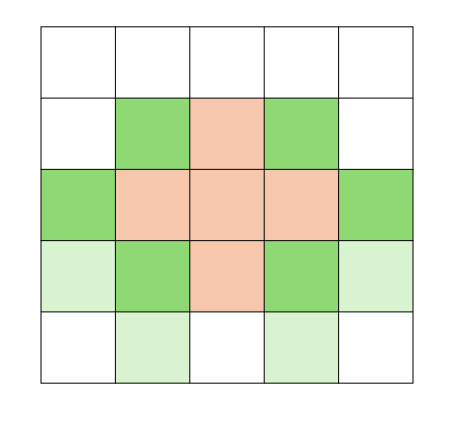
왼쪽 + 아래 이동과 오른쪽 + 아래 이동을 하기위해 빈칸이어야 하는 곳은 위 그림과 같이 그려진다. 천천히 골렘의 위치를 보고 왼쪽으로 한칸씩 아래로 한칸씩 이동해보면 알 수 있다. 이 역시 중앙값을 기준으로 비교하기위해 아래와 같이 배열을 만들어 주었다.
static int[][] downCheck = {{1,-1},{2,0},{1,1}};
static int[][] leftCheck = {{-1,-1},{0,-2},{1,-1},{1,-2},{2,-1}};
static int[][] rightCheck = {{0,2},{-1,1},{1,1},{1,2},{2,1}};
그리고 왼쪽+아래와 오른쪽+아래 이동은 골렘의 방향도 바뀌어야한다. 그냥 어떤식으로 바뀌는지 직접 종이에 그려보면 쉽게 알 수 있다. 아까 위에 그려놨던 golem배열의 인덱스만 바꿔서 다른 골렘으로 그려주면된다. 왼쪽으로 돌때는 (ndir + 3) % 4로 오른쪽으로 돌때는 (ndir + 1) % 4로 계산해서 dir을 바꿔주면 된다.
여기서 조금 더 구체적으로!
이렇게 이동을 진행하는데, if-else문을 사용해 3개 방향 중 1개라도 움직일 수 있으면 움직이도록 만약 3방향 다 움직이지 못한다면 break;를 걸도록 해주었다.
여기서 시간을 너무 많이 잡아먹었는데... 범위를 어떻게 설정해야할지를 몰랐었다. 골렘은 숲의 바깥에서부터 들어오고있고 나는 골렘의 중앙값을 보고있기 때문에 십자인 골렘을 한칸씩 이동시키려면 분명 마이너스 인덱스를 확인해야할텐데 마이너스 인덱스를 사용하면 배열에서 index 오류가 날텐데...? 라는 생각을 했다.
정말 간단하게 그냥 배열을 확장해주면 됐다... 배열을 골렘의 높이만큼인 3을 확장해준다면 이제 위에 3개는 숲의 바깥이 되는것이고 index오류도 안나게 구현이 가능했다..
3. 세 방향 이동 모두 불가능 할때
이렇게 이동을 마치고나면 골렘은 자기가 갈 수 있는 가장 아래에 위치하게 될 것 이다.
이때 해야하는 일이 두가지 있다.
- 현재 골렘이 잘리지 않고 숲속에 다 들어와있는지 확인
- 정령을 이동가능한 가장 낮은 위치로 보내 값 뽑아오기
먼저, 저장된 중앙값을 확인해 골렘의 한군데라도 숲의 바깥에 나가있는지 확인해주면 된다.

굉장히 간단하게 위의 주황색을 바깥이라 생각하고 골렘이 다 들어오려면 4의 위치에 있어야 한다. 현재 위치가 4보다 작다면 조금이라도 잘린거라고 판단하고 숲을 초기화해야한다.
제일 낮은 행으로 이동
이제 제일 낮은 행으로 이동해야한다.
이 부분은 그냥 단순히 dfs로 풀면된다. 중앙에 있던 정령이 이동할 수 있는 위치는 딱 2가지이다.
- 중앙에서 출구로 이동
- 중앙에서 몸통으로 이동
2번 중앙 -> 몸통은 그냥 무시해도 된다.
1번 중앙 -> 출구만 고려하면 되는데, 중앙에서 출구로 이동하면 새로운 골렘에게 옮겨탈 수 있다. 십자모양의 특성상 출구 -> 중앙으로 탈 수 없고 무조건 출구 -> 몸통으로만 탈 수 있다.
이 점을 이용해 중앙 -> 몸통 -> 중앙으로 이동해 방문하지 않은 나머지 부분으로 이동하게 짜주면 된다.
설명하기도 힘든 문제......ㅠㅠ
너무너무 헷갈렸다..........
코드
import java.io.*;
import java.util.*;
public class Main {
static int rSize, cSize;
static int k;
static int[][] forest;
static int[] dy = {-1 ,0, 1, 0};
static int[] dx = {0, 1, 0, -1};
static int[][] place = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}, {0, 0}}; //상, 하, 좌, 우, 중앙
static int[][] golem = {{2, 1, 1, 1, 3},
{1, 1, 1, 2, 3},
{1, 2, 1, 1, 3},
{1, 1, 2, 1, 3}};
static int x, y, ndir;
static boolean[][] visited;
//아래로, 왼쪽아래, 오른쪽아래 체크해야할 것들
static int[][] downCheck = {{1,-1},{2,0},{1,1}};
static int[][] leftCheck = {{-1,-1},{0,-2},{1,-1},{1,-2},{2,-1}};
static int[][] rightCheck = {{0,2},{-1,1},{1,1},{1,2},{2,1}};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
rSize = Integer.parseInt(st.nextToken());
cSize = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
forest = new int[rSize+3][cSize ];
solution(br);
}
private static void solution(BufferedReader br) throws IOException{
int sum = 0;
StringTokenizer st;
for (int i = 0; i < k; i++) {
st = new StringTokenizer(br.readLine());
//x, y는 중앙값
x = 1;
y = Integer.parseInt(st.nextToken()) - 1;
ndir = Integer.parseInt(st.nextToken());
if(moveGolem()){
visited = new boolean[rSize+3][cSize];
int bottom = dfs(x, y) - 2;
sum += bottom;
}else{
clearForest();
}
}
System.out.println(sum);
}
private static int dfs(int x, int y) {
visited[x][y] = true;
int max = x;
if(forest[x][y] == 1){
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(check(nx, ny) && forest[nx][ny] == 3 && !visited[nx][ny]){
max = Math.max(max, dfs(nx, ny));
}
}
}else{
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(check(nx, ny) && forest[nx][ny] != 0 && !visited[nx][ny]){
max = Math.max(max, dfs(nx, ny));
}
}
}
return max;
}
private static boolean moveGolem(){
while(true){
if(canMove(downCheck)){
} else if (canMove(leftCheck)) {
y -= 1;
ndir = (ndir + 3) % 4;
} else if (canMove(rightCheck)) {
y += 1;
ndir = (ndir + 1) % 4;
} else{
break;
}
x += 1;
}
if(x <= 3) return false;
for(int i = 0; i < 5; i++){
int nx = x + place[i][0];
int ny = y + place[i][1];
forest[nx][ny] = golem[ndir][i];
}
return true;
}
private static boolean canMove(int[][] position) {
for (int[] next : position) {
int nx = x + next[0];
int ny = y + next[1];
if(!check(nx,ny) || forest[nx][ny] != 0){
return false;
}
}
return true;
}
static boolean check(int x, int y){
return 0 <= x && x < rSize+3 && 0 <= y && y < cSize;
}
private static void clearForest() {
for (int i = 0; i < rSize + 3; i++) {
for (int j = 0; j < cSize; j++) {
forest[i][j] = 0;
}
}
}
}