[알고리즘] 플로이드-워셜 알고리즘
플로이드-워셜(Floyd-warshall) 알고리즘 쉽게 이해하기
그래프 문제 중, 모든 정점 쌍의 최단 경로를 구하는 문제를 만나면 어떻게 해야할까?
바로 이럴 때 사용되는 알고리즘이 플로이드-워셜 알고리즘이다.
플로이드-워셜이란?
플로이드-워셜은 모든 정점 쌍 간의 최단 거리를 구하는 알고리즘이다.
탐색 중 하나의 정점을 거쳐가는 중간점으로 생각하며, 최단 거리를 계속 갱신해 나간다.
동적 계획법(DP) 기반이고 인접 행렬을 활용해 구현한다.
1. 모든 정점 쌍의 최단 거리 정보가 필요할 때
2. 정점 수가 많지 않을 때 (보통 500이하)
3. 음의 가중치 간선이 있을 수 있을 때 (단, 음수 사이클은 없어야 함)
동작 원리
중간 정점 K를 하나씩 고정하고, 각 정점 i, j에 대해 i -> k -> j 경로가 기존 i -> j 보다 더 짧은지 확인한다.
점화식은 아래와 같다.
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
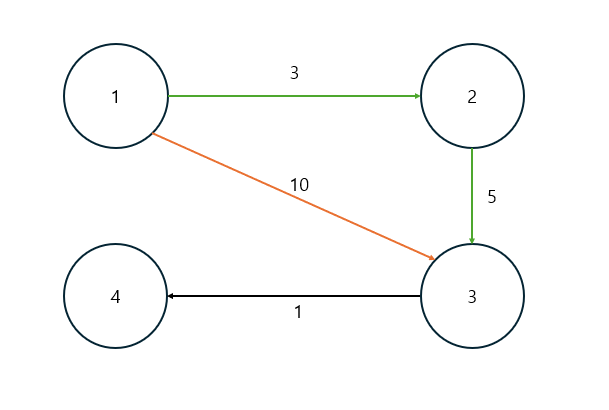
위와같은 그림이 있을 때,
1 -> 3을 가기 위해선 주황 선을 따라 비용이 10이 필요하지만, 1 -> 2-> 3을 가게되면 초록 선을 따라 총 비용이 8이 든다.
이렇게 하나의 정점을 거쳐 갔을 때 최소 비용을 저장하는 방식이다.
만약 이 그림과 다르게 1 -> 4의 간선도 존재하고 만약 비용이 100이라했을 때, 1 -> 2 -> 3 -> 4를 거쳐가는 것보다 비용이 크다.
이런 경우에도 1에서 3을갈때 2를 거쳐가면 비용이 8이 되고, 1 -> 3을 거쳐 4를갈때도 비용이 9로 갱신되면서 이 경우에도 검출이 가능해진다.
예시 문제
도시가 4개 있고, 아래와 같은 경로가 있다고 가정하자.
간선 정보 :
1 -> 2 (비용 4)
1 -> 3 (비용 2)
2 -> 3 (비용 5)
2 -> 4 (비용 10)
3 -> 4 (비용 7)
1단계 : 초기 거리 행렬을 최댓값으로 초기화 진행
| 1 | 2 | 3 | 4 | |
| 1 | 0 | max | max | max |
| 2 | max | 0 | max | max |
| 3 | max | max | 0 | max |
| 4 | max | max | max | 0 |
2단계 : 간선 정보 저장
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 4 | 2 | max |
| 2 | max | 0 | 5 | 10 |
| 3 | max | max | 0 | 7 |
| 4 | max | max | max | 0 |
3단계 : k = 1 (노드 1을 거쳐가는 경우 확인)
1을 거쳐가도 변화 없음.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 4 | 2 | max |
| 2 | max | 0 | 5 | 10 |
| 3 | max | max | 0 | 7 |
| 4 | max | max | max | 0 |
4단계 : k = 2 (노드 2을 거쳐가는 경우 확인)
1 -> 2 -> 4를 거치면 14의 비용으로 4를 갈 수 있음.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 4 | 2 | 14 |
| 2 | max | 0 | 5 | 10 |
| 3 | max | max | 0 | 7 |
| 4 | max | max | max | 0 |
5단계 : k = 3 (노드 3을 거쳐가는 경우 확인)
1 -> 3 -> 4를 거치면 기존 14보다 적은 비용을 쓰고 4를 갈 수 있음.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 4 | 2 | 9 |
| 2 | max | 0 | 5 | 10 |
| 3 | max | max | 0 | 7 |
| 4 | max | max | max | 0 |
6단계 : k = 4 (노드 4을 거쳐가는 경우 확인)
모든 경로가 이미 최소값임.
변화없음.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 4 | 2 | 9 |
| 2 | max | 0 | 5 | 10 |
| 3 | max | max | 0 | 7 |
| 4 | max | max | max | 0 |